Digitale Signaturen Auf Kassenbelegen

Ein Tag in der Sauna 🧖🏽

Vor nicht allzu langer Zeit war ich in der Sauna. Einen ganzen Tag lang legte ich die Füße hoch, las in einem Buch, heizte mich auf und genoss den Tag. Als es dann Zeit wurde zu gehen, fragte der Kassierer, ob ich den Beleg brauche. Ich weiß nicht, was ihr in dieser Situation sagt, aber bei mir ist das immer eine 50/50-Entscheidung. Ich entschied mich an jenem Tag für “Ja.” Auf dem Kassenzettel las ich dann etwas von “ecdsa-plain-SHA384”, was mein Kryptografie-Herz natürlich höher schlagen ließ.

Ein Grund, sich das Ganze also vielleicht etwas genauer anzusehen:

Seit 2020 existiert in Deutschland eine Bonpflicht, die besagt, dass jeder Händler einen Kassenbeleg ausgeben muss. Dadurch soll die Kontrolle von Händlern durch eine Aufsicht vereinfacht werden, um Steuerbetrug effizienter aufzudecken. Kein Wunder also, dass Händler ein Interesse daran haben, die Integrität ihrer Belege zu schützen. Man möchte ja nicht, dass die Konkurrenz Belege fälscht und anschließend Steuerbetrug vorwirft. Um die Integrität digital zu sichern, werden Signatur-Algorithmen verwendet.

Sucht man im Internet nach “ecdsa-plain-SHA384”, so landet man beim “Elektronische(n) Kassenbeleg Standard.” Klar, wie konnte ich so naiv sein zu glauben, in Deutschland gäbe es keine Norm dafür😅🙄; Mein Fehler. Was steht denn da drin?

Der Standard definiert, dass Kassenbelege eine JSON-Struktur haben müssen, also eine simple Zuordnung von einem “Key” (hier “Hashalgorithmus”) zu einem “Value” (hier “ecdsa-plain-SHA384”). Im Kapitel “3.5 Sicherungsdaten (security)” erfährt man dann, dass “Hashalgorithmus” ein Pflichtfeld ist und standardmäßig “ecdsa-plain-SHA256” ist. Soso; Meine Sauna weicht also vom Default ab. Warum? Ich werde es wohl nie erfahren 🤷🏽‍♂️. Immerhin ist “ecdsa-plain-SHA384” ein erlaubter Wert:

Um herauszufinden, was “ecdsa-plain-SHA384” denn jetzt eigentlich bedeutet, muss man sich die “Technische Richtlinie” des Bundesamtes für Sicherheit in der Informationstechnik (BSI) näher anschauen. In TR-03111 wird ganz genau beschrieben, wie digitale Signaturen funktionieren:

“ECDSA” steht für “Elliptic Curve Digital Signature Algorithm” und verrät bereits, dass die Signatur mittels elliptischen Kurven realisiert wird. Elliptische Kurven sind mathematische Objekte, genauer gesagt Funktionen, die “einfach sind in einer Richtung, aber schwierig in die andere.” Als Beispiel: Es ist einfach, eine Person mit Kompass in die Wüste, zu einem vorher vereinbarten Punkt, zu schicken. Setzt man dieselbe Person ohne Kompass an eben jenen Punkt und sagt ihm, er soll zurück, wird er sich vermutlich verlaufen und niemals ankommen (außer er ist James Bond in “Ein Quantum Trost” 📽️😎). Diese Funktionen eignen sich perfekt, um Schlüsselpaare (private und public keys) und somit Signaturen zu realisieren: Man erstellt mit einem private key $P_{private}$ eine Signatur $S$ zu einer Nachricht $M$. Jeder, der den entsprechenden public key $P_{public}$ besitzt, kann verifizieren, dass die Signatur $S$ zur Nachricht $M$ gehört. In der Richtlinie stolpert man auch über “ECGDSA” (Elliptic Curve German Digital Signature Algorithm). Klar, wir kochen natürlich unser eigenes Süppchen 😅😂. Dass sich der Algorithmus kaum von “ECDSA” unterscheidet, überspringe ich jetzt mal.

Nutzt man elliptische Kurven zum Signieren, besteht eine Signatur immer aus zwei Teilen: $(r, s)$. “plain” deutet schlicht an, wie diese zwei Teile formatiert sind, in diesem Fall, einfach “plain” hintereinander geschrieben: $r||s$. Da der Computer weiß, wie lang die Werte sind, weiß er automatisch, wann $r$ aufhört und $s$ beginnt. Neben “plain” gibt es noch andere Formate, um $(r, s)$ mitzuteilen, z.B. das “X9.62” Format:

Zu guter Letzt fehlt also nur noch “SHA-384.” Schaut man sich den Algorithmus zum Erstellen der Signatur genauer an, so fällt auf, dass die Nachricht $M$ “gehasht” wird:

Eine Hash-Funktion weist jeder Nachricht einen Wert mit fixer Länge zu. An sich nicht kompliziert. Ich definiere z.B. $H(M)=42$. Jede Nachricht bekommt den Wert $42$. Um $42$ binär darzustellen, brauche ich 6 Bit ($101010$). Fertig ist meine Hash-Funktion, und ich taufe sie “SHANK-6” 😁. Offensichtlich gibt es gute und schlechte Hash-Funktionen. Gute Hash-Funktionen sind “kollisionsresistent”; bedeutet also jede Nachricht bekommt im besten Fall einen anderen Wert. Da “SHANK-6” jeder Nachricht denselben Wert gibt, ist diese Hash-Funktion also mit die schlechteste, die man nutzen kann 😅. “SHA-384” hingegen ist eine gute Hash-Funktion.

Laut “Toolpage” ist SHA-384 einfach SHA-512 ohne die letzten 128 Bits. Dann bleibt also nur noch herauszufinden, wie SHA-512 berechnet wird: Im Grunde unterteilt man die Nachricht $M$ in Blöcke und komprimiert jeden Block mit dem komprimierten Ergebnis des vorherigen Blocks.

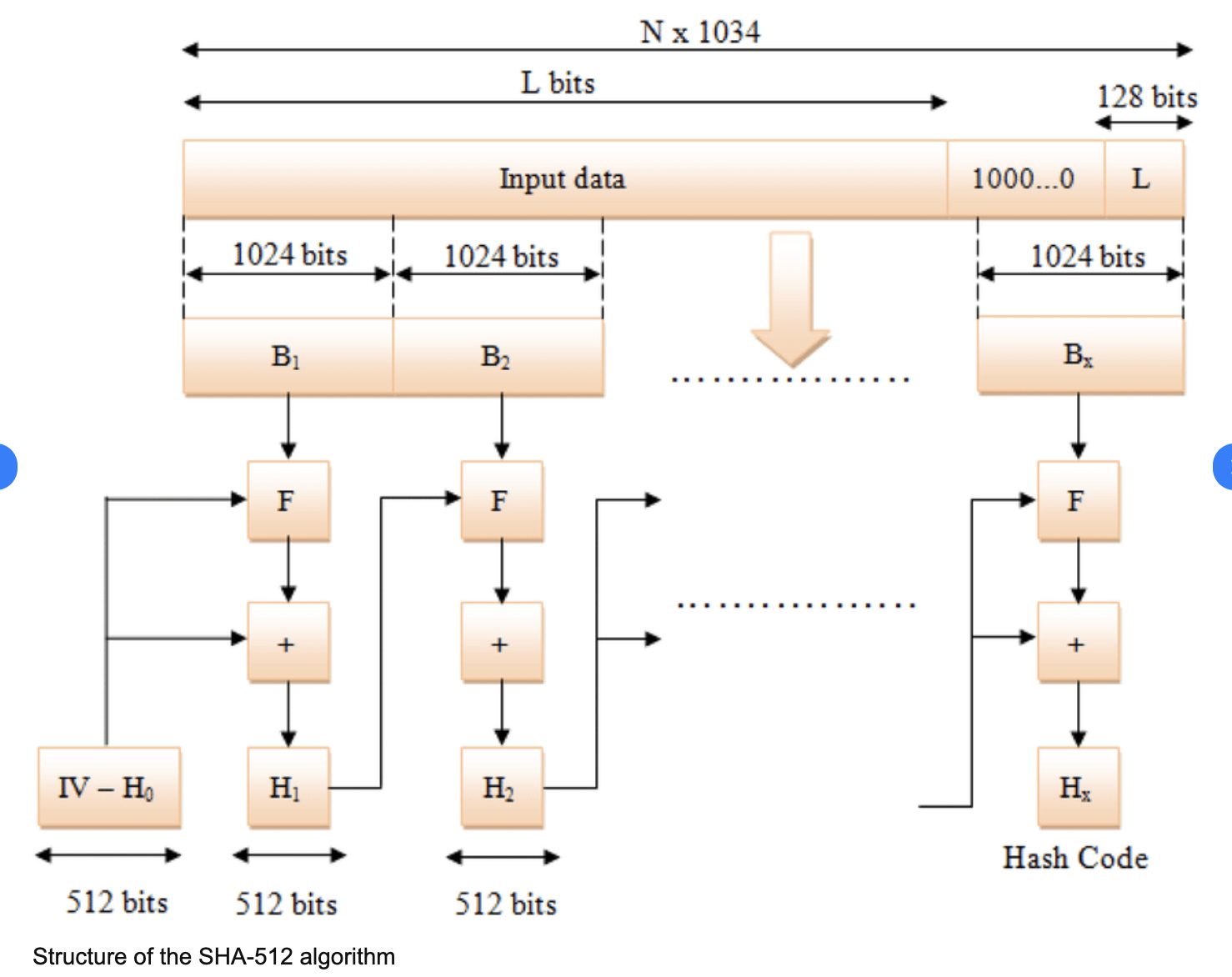
Somit wäre also alles geklärt: Jede Transaktion in einem Laden wird vom Händler, also der Kasse, signiert. Somit kann z.B. eine Kontrollinstanz nachvollziehen, welche Beträge bezahlt worden sind, und dass die entsprechenden Belege von eben jener Kasse erstellt worden sind und niemand anderem. Dazu werden digitale Signaturen verwendet, die auf elliptischen Kurven und einer Hash-Funktion basieren. Um effizient zu sein, führt man Standards und festgelegte Formate ein, z.B. wie die Signatur angeordnet ist (“plain”), oder dass der Beleg im JSON-Format formatiert sein muss.

Faszinierend, wie viel Arbeit, Gedanken und Wissenschaft hinter drei einfachen Wörtern steckt: “ecdsa-plain-SHA384.” Da kann man sich schnell wieder in Details verlieren. Jetzt, da ich wieder etwas schlauer bin, kann ich mich wieder genüsslich meinem Buch widmen, den nächsten Aufguss aufsetzen und getrost die Frage, ob ich den Kassenzettel brauche, mit “Nein” beantworten 😁.

Quellen

• Elektronischer Kassenbeleg Standard
• BSI TR-03111
• Aufbau des SHA-512 Algorithmus
• Aufbau des SHA-384 Algorithmus